|
Server Help
Community forums for Subgame, ASSS, and bots
|
| Author |
Message |
(Deactived B l a h e r)
BiLinux User
I can take it both ways
Age:34
Gender:
Joined: Mar 25 2005
Posts: 341
Location: East Sparta, Ohio
Offline
|
 Posted: Sun Feb 04, 2007 9:28 am Post maybe stupid Post subject: long time no see, I need help with my hw Posted: Sun Feb 04, 2007 9:28 am Post maybe stupid Post subject: long time no see, I need help with my hw |
 |
 |
|
|
Ok, in algebra 2 we were assigned a work assignment.
What we are to do is take a 11"x8.5" paper and make a five sided box out of it.
We are to find a box that can hold the most volume in it. He didn't give anymore instructions on it, but I'm guessing since this is a algebra class and not geometry, the way to find the box with the greatest value is to use some type of equation that has a parabola and the coordinates of the maximum of x will be the side lengths of the box...
I called every body over the weekend, and they just choose a size and went with it hoping it's the biggest in class on Monday. Nobody is even bother with using a equation like me that I have talked to, but I myself am stumbled on how the equation would be set up. I'm guessing the first degree would have to be a negative and a even power.
Can anyone help me set up or give me a hint to use a equation to find it?
EDIT: BTW, I left my graphing calculator at school...
|
|
| Back to top |
|
 |
CypherJF
I gargle nitroglycerin

Gender:
Joined: Aug 14 2003
Posts: 2582
Location: USA
Offline
|
 Posted: Sun Feb 04, 2007 10:12 am Post maybe stupid Post subject: Posted: Sun Feb 04, 2007 10:12 am Post maybe stupid Post subject: |
 |
 |
|
|
You shouldn't be needing a graphing calculator in algebra 2 anyway, meh.
_________________
Performance is often the art of cheating carefully. - James Gosling
|
|
| Back to top |
|
 |
Dr Brain
Flip-flopping like a wind surfer

Age:39
Gender:
Joined: Dec 01 2002
Posts: 3502
Location: Hyperspace
Offline
|
 Posted: Sun Feb 04, 2007 11:53 am Post maybe stupid Post subject: Posted: Sun Feb 04, 2007 11:53 am Post maybe stupid Post subject: |
 |
 |
|
|
The thing to realize is that you're cutting equal sized squares out of the 4 corners before you fold it up. That means there's only 1 variable to work with.
height = the side of the square, call it x.
width = 8.5 - 2*x
length = 11 - 2*x
V(x) = h*w*l = (x)(8.5 - 2x)(11 - 2x)
Factor:
V(x) = (4x)(x-5.5)(x - 4.25)
Then just use the methods you've been taught to find the max of the cubic. I've forgotten because I know calculus and it's so much easier as a min-max problem.
_________________
Hyperspace Owner
Smong> so long as 99% deaths feel lame it will always be hyperspace to me
|
|
| Back to top |
|
 |
Animate Dreams
Gotta buy them all!
(Consumer whore)

Age:37
Gender:
Joined: May 01 2004
Posts: 821
Location: Middle Tennessee
Offline
|
 Posted: Sun Feb 04, 2007 12:32 pm Post maybe stupid Post subject: Posted: Sun Feb 04, 2007 12:32 pm Post maybe stupid Post subject: |
 |
 |
|
|
| Dr Brain wrote: | | I've forgotten because I know calculus and it's so much easier as a min-max problem. |
Yeah, this looked like a calculus problem to me, when I first looked at it. Really, why don't they start teaching Calculus when they start teaching Algebra? As long as they only taught the amount of Calculus you could do at an Algebra level then, I think it would be fine. Calculus is easy, too.
Or... it would be, if I had ever bothered to take a trig class. Or show up to Algebra II. But my biggest problem with Calculus is that I'll finish a problem, and it looks completely wrong so I just erase it all. Then once we get the answers back, it turns out I had everything right. >_>
|
|
| Back to top |
|
 |
lazy_Blaher
Guest
Offline
|
 Posted: Sun Feb 04, 2007 1:10 pm Post maybe stupid Post subject: Posted: Sun Feb 04, 2007 1:10 pm Post maybe stupid Post subject: |
 |
 |
|
|
thanks brain, I got i now.
I'm guessing when you say V(x) it's just the function of x, right?
I'm of to go factor, thanks again.
|
|
| Back to top |
|
 |
Guest
Offline
|
 Posted: Sun Feb 04, 2007 1:15 pm Post maybe stupid Post subject: Posted: Sun Feb 04, 2007 1:15 pm Post maybe stupid Post subject: |
 |
 |
|
|
| yea, nvm. I'm not thinking. I'm just beings stupid. don't asnwer the fucntion of x thing.
|
|
| Back to top |
|
 |
Mine GO BOOM
Hunch Hunch
What What

Age:42
Gender:
Joined: Aug 01 2002
Posts: 3615
Location: Las Vegas
Offline
|
 Posted: Mon Feb 05, 2007 1:32 am Post maybe stupid Post subject: Posted: Mon Feb 05, 2007 1:32 am Post maybe stupid Post subject: |
 |
 |
|
|
Does the box need to be folded, or can it be loose pieces taped at all the sides? If you can use tape to hold sides together, get three pieces of 11" by 8.5" paper and cut out five squares that are sqrt(187/10) (~4.32435) width and length, and tape into a 5 sided box.
When your teacher mentions that you used more than one piece of paper, explain to him that the box you have represents cutting up a single piece of paper into a bunch of really small piece that you taped together to form the correct dimensions. If he still mentions that this is invalid and that you used more than one piece of paper, say that the surface amount of paper you used to make your box (which is the peak volume of sqrt(187/10)^3 or ~80.8653 in^3) is just 5 * sqrt(187/10) * sqrt(187/10), which equals 93.5 in^2, the same as 11" * 8.5".
If you want to know why 80.8653 in^3 is the max, I could show you a bunch of linear algebra to explain min/max problems, but the easiest way is just to think of it logically. What is the most optimal shape for volume? Sphere, well, we want a box, so it must have 5 sides. That gets us to 5 * x = 93.5. x has to be a rectangle, so we want the greatest surface area for x = w * l. To get that, w should be equal to l, so x = w^2. Throw that back up a line, and you get 5 * w^2 = 93.5. Solve for w, and you get sqrt(187/10), or ~4.32435. This brings us to needing the volume, which is just w * l * h, which are all the same since we are using squares for each side, so sqrt*(187/10)^3 = ~80.8653 inches cubed.
That would be my answer, because I'm a jackass and like to go about tasks the way that would piss the teacher off the most. If they didn't allow this, but did allow the five sides to be whole, loose rectangles cut from the same piece of paper, it is a bit more complex, and I would have to go into linear algebra which is beyond your class right now, but brings you pretty close to the maximum volume. If you all sides of the box have to be attached and are folded into a 5-sided box, Dr Brain's method is correct, and can be done at your level. It brings you nearly 80% of your theoretical maximum volume, but I can't give you a direct answer then it is just a simple equation to solve for x. To help narrow your search, 1" <= x <= 2".
|
|
| Back to top |
|
 |
Default
Server Help Squatter

Age:44
Gender:
Joined: Aug 25 2005
Posts: 286
Offline
|
 Posted: Tue Feb 06, 2007 5:44 am Post maybe stupid Post subject: Posted: Tue Feb 06, 2007 5:44 am Post maybe stupid Post subject: |
 |
 |
|
|
| Oh my now you need to be help doing your homework, that unusal. Aint these for Subspace / Continuum server help or what lol....
|
|
| Back to top |
|
 |
(Deactived B l a h e r)
BiLinux User
I can take it both ways
Age:34
Gender:
Joined: Mar 25 2005
Posts: 341
Location: East Sparta, Ohio
Offline
|
 Posted: Tue Feb 06, 2007 10:10 pm Post maybe stupid Post subject: jackass, just like me Posted: Tue Feb 06, 2007 10:10 pm Post maybe stupid Post subject: jackass, just like me |
 |
 |
|
|
no, he specifically said we can make cuts in it to fold the ends up, but it has to stay one piece. I was already ahead of you when he first brought it up, but then I got mad when he started to give guild lines.
Default, yes, no, yes, yes, and no. It's trash talk, nobody really cares. Besides I didn't know any other places a the time, and this is probably the best place I can think of.
I factored the solution down to:
V(x)=4x^4-22x^3+76.5x^2
but that just doesn't seem right, and I'm waiting for a non-snow day so I can go get my calculator to graph it. I'm a little bit tired, and I don't think I'm going to know what to do next, but maybe when I do it, it'll hit me. As for then, I'm just going to sit back and enjoy my snow day.
|
|
| Back to top |
|
 |
Samapico
No, these DO NOT look like penises, ok?

Joined: May 08 2003
Posts: 1252
Offline
|
 Posted: Tue Feb 06, 2007 11:08 pm Post maybe stupid Post subject: Posted: Tue Feb 06, 2007 11:08 pm Post maybe stupid Post subject: |
 |
 |
|
|
http://www.coolmath.com/graphit
That's the first to come up on google, there are probably other better java applets for that.
_________________
(Insert a bunch of dead links here)
|
|
| Back to top |
|
 |
Mine GO BOOM
Hunch Hunch
What What

Age:42
Gender:
Joined: Aug 01 2002
Posts: 3615
Location: Las Vegas
Offline
|
 Posted: Tue Feb 06, 2007 11:52 pm Post maybe stupid Post subject: Re: jackass, just like me Posted: Tue Feb 06, 2007 11:52 pm Post maybe stupid Post subject: Re: jackass, just like me |
 |
 |
|
|
| blah-er wrote: | I factored the solution down to:
V(x)=4x^4-22x^3+76.5x^2 |
Where the hell did you get that? He gave you the factored version, V(x) = (4x)(x-5.5)(x - 4.25)
To make sure you get a bit further along, here is it graphed between a volume of 0 to a volume of 0 (Y axis). Along the X axis is the length of each square you'll cut out of each corner. Notice it is between the 1" and 2" marks, like I mentioned before, but it is not a nice roundish number like 1.5". Either read up a bit of how to find a maximum value of a function, or use a random application you can find.
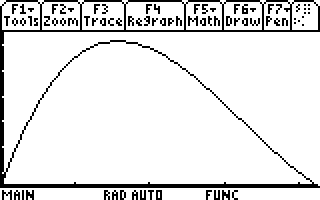
 screen.png - 1.39 KB
screen.png - 1.39 KB
File downloaded or viewed 23 time(s)
|
|
| Back to top |
|
 |
(Deactived B l a h e r)
BiLinux User
I can take it both ways
Age:34
Gender:
Joined: Mar 25 2005
Posts: 341
Location: East Sparta, Ohio
Offline
|
 Posted: Wed Feb 07, 2007 6:32 am Post maybe stupid Post subject: oppsy Posted: Wed Feb 07, 2007 6:32 am Post maybe stupid Post subject: oppsy |
 |
 |
|
|
opps, I factored V(x) = h*w*l = (x)(8.5 - 2x)(11 - 2x) .
Got though, thanks. I knew that problem was weird for some reason.
There's already a simple tool on my calc that finds the maximum.
So, I'll have that taken care of in a quick fix.
Remember kids, don't be stupid like me and forget your GCF!
|
|
| Back to top |
|
 |
|
|
You can post new topics in this forum
You can reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
You cannot attach files in this forum
You can download files in this forum
|
Software by php BB © php BB Group
Server Load: 25 page(s) served in previous 5 minutes. |